A small body slips, subject to the force of friction, from point $A$ to point $B$ along two curved surfaces of equal radius, first along route $1,$ then along route $2$. Friction does not depend on the speed and the coefficient of friction on both routes is the same. In which case will the body’s speed at $B$ be greater?
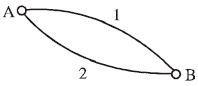
A small body slips, subject to the force of friction, from point $A$ to point $B$ along two curved surfaces of equal radius, first along route $1,$ then along route $2$. Friction does not depend on the speed and the coefficient of friction on both routes is the same. In which case will the body’s speed at $B$ be greater?

- A
speed is greater in case $1$
- B
speed is greater in case $2$
- C
speed is same in both cases
- D
cannot be determined
Similar Questions
Which of the following is self adjusting in nature?
Which of the following is self adjusting in nature?
As shown in the figure, a block of mass $\sqrt{3}\, kg$ is kept on a horizontal rough surface of coefficient of friction $\frac{1}{3 \sqrt{3}}$. The critical force to be applied on the vertical surface as shown at an angle $60^{\circ}$ with horizontal such that it does not move, will be $3 x$. The value of $3x$ will be
$\left[ g =10 m / s ^{2} ; \sin 60^{\circ}=\frac{\sqrt{3}}{2} ; \cos 60^{\circ}=\frac{1}{2}\right]$
As shown in the figure, a block of mass $\sqrt{3}\, kg$ is kept on a horizontal rough surface of coefficient of friction $\frac{1}{3 \sqrt{3}}$. The critical force to be applied on the vertical surface as shown at an angle $60^{\circ}$ with horizontal such that it does not move, will be $3 x$. The value of $3x$ will be
$\left[ g =10 m / s ^{2} ; \sin 60^{\circ}=\frac{\sqrt{3}}{2} ; \cos 60^{\circ}=\frac{1}{2}\right]$
- [JEE MAIN 2021]
Why are mountain roads generally made winding upwards rather than going straight up ?
Why are mountain roads generally made winding upwards rather than going straight up ?
A block of mass $5\,kg$ and surface area $2\,m ^2$ just begins to slide down an inclined plane when the angle of inclination is $30^{\circ}$. Keeping mass same, the surface area of the block is doubled. The angle at which this starts sliding down is :
A heavy body of mass $25\, kg$ is to be dragged along a horizontal plane $\left( {\mu = \frac{1}{{\sqrt 3 }}} \right).$ The least force required is ........ $kgf$
A heavy body of mass $25\, kg$ is to be dragged along a horizontal plane $\left( {\mu = \frac{1}{{\sqrt 3 }}} \right).$ The least force required is ........ $kgf$
